MATHCAD 6.0 SE
Dieter Reiermann
Mathcad ist das erste Formelbearbeitungsprogramm, das Texte, Grafiken und mathematische Ausdrücke in „druckreifer“ Form auf dem Bildschirm darstellt.
In einem Mathcad-Dokument können Texte, Grafiken, Formeln, Diagramme an beliebigen Stellen im Dokument plaziert werden. Jeder Bereich hat seine spezifischen Bearbeitungsmöglichkeiten. Die Menü-Auswahl, die Palettenleiste und die darunter befindliche Symbolleiste am oberen Bildschirmrand ermöglichen ganz intuitiv Mathcad in kurzer Zeit „in den kleinen Finger“ zu bekommen.
Die Auswahl der zu editierenden Bereiche erfolgt einfach durch Mausklick! (siehe Screenshots)
FIRST STEPS
Erste Schritte mit Mathcad: Die ersten Beispiele zeigen, wie die Berechnung eines Zahlenwertes aus einer Formel “druckreif” auf dem Arbeitsblatt erfolgen kann:
Gerechnet wird sofort, wenn der AUTO-Mode eingeschaltet ist (Anzeige rechts unten).
Sonst muß «ALT¦R»«B» bzw. «F1» aktiviert werden!
Editieren von Variablen: Kursor auf den Variablennamen setzen und mit «à» oder «á» das zu ändernde Zeichen anfahren.
Editieren von Formelzeichen und Operatoren: Ausdruck, für den der Operator (das Formelzeichen) gilt, anklicken und mit den «â» oder «ã»-Tasten umfassen.
Nach «Del» erscheint ein Platzhalter, auf den der neue Operator gesetzt werden kann.
Verschieben von Regionen: mit MAUS LINKS Cursor in den Textbereich oder Formelbereich hineinziehen, dann die strichlierte Box plazieren (DRAG & DROP).
Beispiel1
Es ist der Gesamtwiderstand Rg der Schaltung zu berechnen:
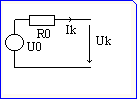
Der Angabetext wird nach einem Anführungszeichen getippt, die Graphik kann über die Zwischenablage geholt werden oder mit «ALT¦G¦B» und Eintrag des Dateinamens in den Platzhalter des Bildrahmens importiert werden.
PABLITOS
Beispiel 2
Zeichne die Kurve
Formelbereiche können in Textbereiche eingebettet werden: Nach «"» wird Text geschrieben und mit «ALT¦T¦B» ein Platzhalter für die Formel erzeugt.
Schreiben der Formel:
y(x):x/x^2+1/3«â»«â»«â»«â»«Wurzelzeichen aus Taschenrechnerpalette»
Bereichsangabe: Die Bereichsangabe x:0,1/4;10 Sprich: von 0 über ¼ (in Stufen von ¼) bis 1
Diagramme: Diagramme werden mit «@» rechts neben dem Cursor positioniert, in die Platzhalter werden x und y(x) eingetragen. Vergrößern durch Anfahren mit der Maus bei gedrückter linker Taste und Ziehen am Doppelpfeil unten, an der Ecke rechts unten oder rechts.
Rechenreihenfolge
Mathcad rechnet immer zuerst von links nach rechts, dann Zeile für Zeile, also genauso wie man liest. Wenn ein Rechenobjekt, z.B. eine Matrix oder ein Diagramm vertikal etwas mehr Platz braucht, so muß es trotzdem hinter dem vorherigen Rechenschritt beginnend angeordnet sein.
FALSCH: linker oberer Eckpunkt des Bereiches oberhalb der Bereichsdefinition!
RICHTIG
Globale Definitionen
Mit dem º definierte globale Variablen gelten überall im Dokument von der ersten Zeile an:
Frame 430
Die Auswertung steht vor der globalen Definition.
Damit können Funktionen z.B. auf der Nebenseite rechts oder der letzten Seite des Dokumentes (im Anhang) global definiert werden und davor im ganzen Dokument verwendet werden. Besonders nützlich sind globale Definitionen, wenn Konstante, zB. Einheiten definiert werden müssen, wobei die Definition nicht im Ausdruck aufscheinen soll. In diesem Fall wird bei SEITE EINRICHTEN, BIS ZUM RECHTEN RAND gewählt bzw. «ALT¦D»«E»«ALT¦I»
|
U=10µV (Die Definition für uV kann auch auf der rechten Nebenseite stehen ) |
|
Numerische Auswertung von Brüchen
Mit SYMBOLISCH AUSWERTEN «ALT¦S»«U»«W» wird das Ergebnis wieder ein Bruch.
Vektoren
Mathcad bietet zahlreiche Möglichkeiten zur Rechnung mit Vektoren und Matrizen. Die Eingabe erfolgt über die Matrizenpalette bzw. über «CTRL¦M». Spaltenvektoren sind grundsätzlich Matrizen mit einer Spalte.
Damit wird eine Indizierung ab 1 erzwungen. «ALT¦R»«V»
|
Elemente |
Skalares Produkt |
Vektorielles Produkt |
|
|
|
|
|
Betrag |
Multiplikation mit Skalar |
|
|
|
Beispiel zur Anwendung des mathematischen Zeichensatzes
Die nachstehenden komplexen Vektoren wurden mit «ALT¦R»«C» .... unterstrichen dargestellt:
Zuerst wurde mit "Komplex" eine neues Schriftartattribut definiert, dann die komplexen Variablen ausgewählt und mit «ALT¦R»«C» einzeln durch Auswahl des Attributes unterstrichen dargestellt.
Vektorisieroperator
Der Vektorisieroperator wird für elementweise Operationen auf Vektoren oder Matrizen angewendet:
Frame 318Matrizen
Matrizenrechnung sei anhand der Lösung eines Gleichungssystems gezeigt:
|
|
|
|
|
|
Ein- und Ausgabe
mit Tabellen
Tabellen können als Ergebnis von Berechnungen erzeugt werden, die über einen Wertebereich durchgeführt werden:
|
|
|
|
|
ÚÄÄÄ¿ ³0.1³ ÃÄÄÄ´ ³0.5³ ÃÄÄÄ´ ³0.9³ ÃÄÄÄ´ ³1.3³ ÃÄÄÄ´ ³1.7³ ÃÄÄÄ´ ³2.1³ ÃÄÄÄ´ ³2.5³ ÀÄÄÄÙ |
ÚÄÄÄÄ¿ ³0.01³ ÃÄÄÄÄ´ ³0.25³ ÃÄÄÄÄ´ ³0.81³ ÃÄÄÄÄ´ ³1.69³ ÃÄÄÄÄ´ ³2.89³ ÃÄÄÄÄ´ ³4.41³ ÃÄÄÄÄ´ ³6.25³ ÀÄÄÄÄÙ |
ÚÄÄÄÄÄÄ¿ ³-1 ³ ÃÄÄÄÄÄÄ´ ³-0.301³ ÃÄÄÄÄÄÄ´ ³-0.046³ ÃÄÄÄÄÄÄ´ ³ 0.114³ ÃÄÄÄÄÄÄ´ ³ 0.23 ³ ÃÄÄÄÄÄÄ´ ³ 0.322³ ÃÄÄÄÄÄÄ´ ³ 0.398³ ÀÄÄÄÄÄÄÙ |
|
|
|
|
|
ÚÄÄÄÄÄÄÄ¿ ³- 0.01 ³ ÃÄÄÄÄÄÄÄ´ ³- 0.83 ³ ÃÄÄÄÄÄÄÄ´ ³-17.702³ ÃÄÄÄÄÄÄÄ´ ³ 14.832³ ÃÄÄÄÄÄÄÄ´ ³ 12.541³ ÃÄÄÄÄÄÄÄ´ ³ 13.686³ ÃÄÄÄÄÄÄÄ´ ³ 15.706³ ÀÄÄÄÄÄÄÄÙ |
ÚÄÄÄ¿ ³1.1³ ÃÄÄÄ´ ³1.5³ ÃÄÄÄ´ ³1.9³ ÃÄÄÄ´ ³2.3³ ÃÄÄÄ´ ³2.7³ ÃÄÄÄ´ ³3.1³ ÃÄÄÄ´ ³3.5³ ÀÄÄÄÙ |
ÚÄÄÄÄÄ¿ ³1.1 m³ ÃÄÄÄÄÄ´ ³1.5 m³ ÃÄÄÄÄÄ´ ³1.9 m³ ÃÄÄÄÄÄ´ ³2.3 m³ ÃÄÄÄÄÄ´ ³2.7 m³ ÃÄÄÄÄÄ´ ³3.1 m³ ÃÄÄÄÄÄ´ ³3.5 m³ ÀÄÄÄÄÄÙ |
Eine Tabelle wird nur mit maximal 50 Zeilen angezeigt.
Einheiten werden zu jedem Eintrag eingefügt, wenn nicht der zugehörige Ausdruck durch die Einheit dividiert wird (siehe Spalte )
Eingangswerte in Tabellen
Auch Eingangswerte können in Tabellen eingetragen werden:
Frame 365
Eingrenzung
des Wertebereichs
Zur Eingrenzung des Wertebereiches gibt es relationale Operatoren
("="-Palette
):
Zur Vermeidung von Singularitäten:
Stückweise stetige Funktionen
Diagramme
Mathcad bietet eine ganze Reihe von Diagrammausgaben an:
Die x-y-Darstellung
Cursor für die linke obere Ecke der Grafik positionieren, dann «@» oder «ALT¦G»«Y». Eintrag der Variablen bzw. Ausdrücke für die Abszisse in die Platzhalter unterhalb mittig bzw. links neben der Ordinate mittig. Die darzustellenden Bereiche können an an den links und rechts von der Abszisse bzw. unten und oben von der Ordinate befindlichen Platzhaltern eingetragen werden. Weitere Ausdrücke auf der y-Achse werden, durch Beistrich getrennt, eingetragen.
Drei Perioden einer Sinuskurve (p...«CTRL¦P»)
Nach Eintragen der unabhängigen Variablen auf den Abszissenplatzhalter und der Funktion auf den Ordinatenplatzhalter erscheint die Grafik auf dem Bildschirm. Die Größe und der Ort der Grafik kann mit der DRAG & DROP-Methode verändert werden.Dazu wird die Grafik zuerst mit der strichlierten Box umgeben und durch Ziehen am unteren oder rechten Rand der Box (bei gedrückter Maustaste) in der Größe verändert.Ein Verschieben der gesamten Grafik wird durch Anklicken der Region und Ziehen der Box erreicht. Der Zahlenbereich der Achsen kann auf ihren Platzhaltern angegeben werden.
Für XY-Diagramme gibt es zahlreiche Möglichkeiten der Gestaltung, wie unter anderem Farben-, Linien-und Diagrammformatwahl.
Frame 353Parameterdarstellung
Frame 563
Lissajousche Figur: y durchläuft im Intervall i=1..51 3 mal soviele Schwingungen wie x. In der Elektrotechnik können L.F. zur Beobachtung von Frequenzverhältnissen verwendet werden.
Polardiagramme
Frame 566
Parameterdarstellung im XY-Diagramm
Mehr als ein Graph
Beide Achsen können aber auch mehrere Ausdrücke tragen: Momentanwert der Spannung u(t), des Stromes i(t) und der Wechselleistung p(t):
Koordinaten ablesen
In einem ausgewählten Diagramm können mit einem Fadenkreuz Koordinaten abgelesen werden. Nach «ALT¦X»«O» muß der Cursor an den gewünschten Punkt der Grafik gebracht werden. Nach Mausklick kann abgelesen werden. Die Kopien der Ablesewerte bekommt man aus der Zwischenablage.
3-D Diagramme
Dreidimensionale Diagramme werden prinzipiell mittels Matrizen dargestellt. Zur Auswahl stehen das Flächendiagramm, das Säulendiagramm, das Umrissdiagramm, das Punktdiagramm.Für alle 3D-Diagramme gibt es zahlreiche Variationsmöglichkeiten.Die Betrachtungrichtung kann über Winkel für Rotation und Neigung verändert werden: «ALT¦G»«D».
Die Fläche wird für 21 mal 21 Grundflächenpunkte aufgebaut!
Vektordiagramme
Vektorfelddiagramme benötigen 2 Matrizen, z.B. die Real- und die Imaginärteilmatrix einer komplexen Matrix:
Streuungsdiagramm
Die Position der Punkte eines Streuungsdiagramms wird durch 3 Vektoren beschrieben, zB. einen X-Vektor, einen Y-Vektor und einen Z-Vektor:
Es werden 16 Zufallszahlen im Bereich 0 bis 50 erzeugt.
Parameterflächen
Es müssen 3 Matrizen für die Transformation von Punkten aus der Zeichenebene in die 3D-Darstellung formuliert werden:
i,j...Koordinaten der Zeichenebene.
Die Lage eines Raumpunktes (x,y,z) der Fläche steht für alle 3 mal 32 Punkte in den Matrizen X, Y, Z
Animationen
Wenn der zu transformierende Bereich dynamisch über die Variable FRAME vergrößert wird, kann mit ALT F eine Animation ( hier das „Wachsen“ des Bandes ) erstellt werden:
Wichtig: Die zu animierende Grafik muß nach Einstellen der Parameter im
Animationsmenü mit einem strichlierten Kästchen ausgewählt werden. Erst
dann wird die Berechnung der einzelnen Bilder gestartet. Das Ergebnis wird
über die MM-Schnittstelle (Media-Player) kontrolliert und kann dann zB.
im AVI-Format abgespeichert werden. Die Wiedergabe ist ebenso aus dem Animationsmenü
möglich:
«ALT¦F»«N»«W»