Da es zwischen den einzelnen Funktionen sehr viele Zusammenhänge gibt, finden sich in den einzelnen Abschnitten sehr viele Verweise auf andere Punkte. Es wurde von den Verfassern dieses Skriptums versucht, die Übersicht so gut wie möglich zu wahren. Aus Gründen der Verständlichkeit wird daher empfohlen, die zur Verfügung gestellten Beispiele unbedingt durchzuarbeiten.

Die im Syntax der einzelnen Funktionen fett dargestellten Argumente müssen unbedingt eingegeben werden, die dünn gedruckten Argumente können eingegeben werden.

1.2 Allgemeines

Es ist darauf zu achten, dass für Zins (Zinssatz pro Periode, siehe Punkt ) und Zzr (Anzahl der Zahlungszeiträume) von der gleichen Zeitbasis ausgegangen wird.

(z.B. Gefahr bei jährlichem Zinssatz und monatlicher Zahlung mit 2 jähriger Laufzeit, denn hier müsste der Zinssatz Zins durch 12 dividiert, und die Laufzeit Zzr mit 2 multipliziert werden.).

Für Annuitätenfunktionen[1] gilt, dass Zahlungen, die getätigt werden durch negative Zahlen, eingenommene Beträge durch positive Zahlen dargestellt werden.

1.3 BW (PV)

Der Barwert BW berechnet den aktuellen Wert einer Reihe zukünftiger Zahlungen und liefert den Barwert einer Investition. Die nachfolgenden Zahlungen werden mit dem Periodenzins exponentiell abgezinst.

Eine wichtige Bedingung ist, dass es regelmäßige Zahlungen in gleicher Höhe und immer gleichen zeitlichen Abständen sind.

=BW(Zins;Zzr;Rmz;Zw;F) oder engl. =PV(rate;nper;pmt;fv;type)

Zins ist der Zinssatz pro Periode (=Zahlungszeitraum). Näheres siehe Punkt 7.

Zzr gibt an, über wie viele Perioden die jeweilige Annuität (=Rente) gezahlt wird. Zzr ist die Anzahl der Zahlungszeiträume. Näheres siehe Punkt 9.

Rmz ist der konstante Betrag (Annuität), der in jeder Periode gezahlt wird. Rmz bedeutet regelmäßige, konstante Zahlungen. Näheres siehe Punkt 11.

Zw ist der zukünftige Wert (Endwert) oder der Kassenbestand, den man nach der letzten Zahlung erreicht haben möchte. Näheres siehe Punkt 10.

F bedeutet Fälligkeit und kann nur die Werte 0 oder 1 annehmen. 0 oder nicht angegeben bedeutet, dass die Zahlungen am Ende der Periode fällig sind. Eine 1 hingegen bedeutet, dass die Fälligkeit der Zahlungen am Anfang der Periode ist.

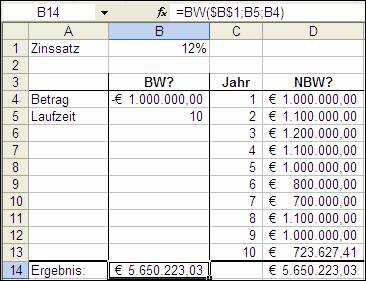
Abbildung 1: Ausschnitt aus dem Beispiel für Barwert

1.4 IKV (IRR)

Durch den IKV wird der interne Zinsfuß einer Investition berechnet. Zinsfuß ist der Zinssatz, der für eine Investition erreicht wird, die in regelmäßigen Abständen erfolgt. Die Zahlungen müssen nicht gleich groß sein, jedoch der Zinsfuß muss in regelmäßigen Intervallen auftreten.

=IKV(Werte;Schätzwerte) oder engl. =IRR(values;guess)

Werte ist eine Matrix von Zellen oder ein Bezug von Zellen, in denen Zahlen stehen, für die man den internen Zinsfuß berechnen möchte. Sie muss mindestens einen positiven und einen negativen Wert enthalten. Enthält die Matrix Text, Wahrheitswerte oder leere Zellen, werden diese Werte ignoriert.

IKV nimmt an, dass die Zahlungen in der Reihenfolge erfolgen, in der sie in „Werte“ gegeben sind.

Schätzwert ist eine Zahl, von der man annimmt, dass sie dem Ergebnis nahe kommt.

Kann IKV kein geeignetes Ergebnis finden, wird der Fehlerwert „#Zahl!“ angezeigt. Diesen Fehler kann man beheben, indem man den Schätzwert verändert.

In den meisten Fällen ist es nicht erforderlich den Schätzwert anzugeben. Wird er nicht angegeben, wird er als 10% vom Ergebnis angenommen.

1.5 KAPZ (PPMT)

KAPZ liefert die Kapitalrückzahlung (Tilgung) einer Investition für die angegebene Periode. Ein konstanter Zinssatz und konstante periodische Zahlungen werden vorausgesetzt.

Die Funktion ermittelt den Tilgungsanteil der x-ten Annuität.

=KAPZ(Zins;Zr;Bw;Zw;F) oder engl. =PPMT(rate;per;nper;pv;fv;type)

Die Bedingungen sind analog zu denen des BWs.

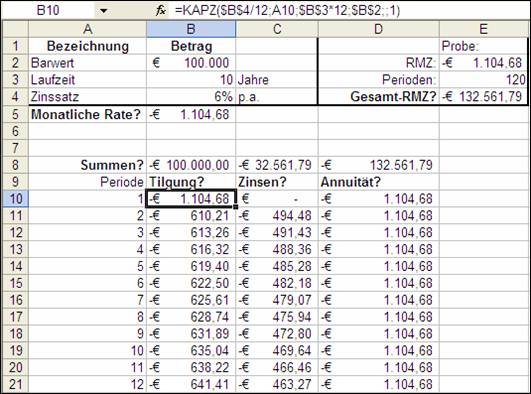
Abbildung 2: Ausschnitt aus dem Beispiel für Kapitalrückzahlung

1.6 NBW (NPV)

NBW errechnet den Nettobarwert einer Investition mit Hilfe eines Abzinsungsfaktors.

=NBW(Zins; Wert1; Wert2;...) oder engl. =NPV(rate;value1;value2;…)

Wert 1; Wert 2 sind unterschiedlich hohe Zahlungen, die aber regelmäßig am Ende der Periode getätigt werden. Dazu gehören Einzahlungen und Auszahlungen. Damit der richtige NBW ermittelt werden kann, müssen die Zahlungen in der richtigen Reihenfolge stehen.

Weiters ist es wichtig, dass leere Zellen, Wahrheitswerte, Texte oder Fehlerwerte in einer Matrix ignoriert werden.

Die Grundlage des NBW sind zukünftige Zahlungen. Eine Investition, die mit NBW errechnet wird, beginnt eine Periode vor der Leistung des Wert 1. Beendet wird sie mit dem letzten Wert. Erfolgt eine Zahlung schon in der ersten Periode, dann darf sie nicht zu den Werten hinzugefügt werden, sondern muss zum Ergebnis addiert werden.

NBW ist vergleichbar mit BW. Der Unterschied besteht darin, dass bei BW die Zahlungen sowohl am Anfang, als auch am Ende der Periode beginnen können, aber dafür konstante Beträge sein müssen. Bei NBW hingegen können variable Zahlungen stattfinden.

NBW ist außerdem mit der Funktion IKV verwandt. IKV berechnet den Zinssatz, für den der NBW einer Investition den Wert 0 annimmt:

=NBW(IKV(...);...)=0

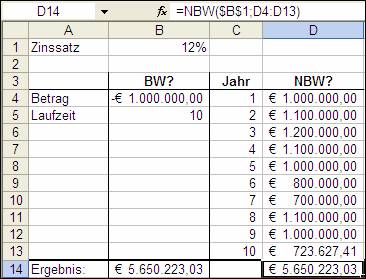
Abbildung 3: Ausschnitt aus dem Beispiel für Nettobarwert

1.7 ZINS (RATE)

ZINS liefert den Zinssatz einer regelmäßigen Zahlung mithilfe eines Iteratiosverfahren wobei keine oder mehrere Lösungen möglich sind.

=ZINS(Zzr;Rmz;Bw;Zw;F;Schätzwert)

oder engl. =RATE(nper;pmt;pv;fv;type;guess)

Zzr bedeutet Anzahl der Zahlungszeiträume. Die genaue Beschreibung ist unter Punkt 9 zu finden.

RMZ bedeutet regelmäßige Zahlung. Die genaue Beschreibung ist unter Punkt 11 zu finden.

BW bedeutet Barwert. Die genaue Beschreibung ist unter Punkt 3 zu finden.

ZW bedeutet zukünftiger Wert und stellt praktisch den Endwert dar. Genaueres siehe Punkt 10.

F bedeutet Fälligkeit und kann entweder den Wert 0 oder den Wert 1 annehmen. Wird der Wert 0 eingesetzt oder keine Fälligkeit angegeben, so geht Excel vom Anfang der Periode aus, wird 1 eingetragen, geht Excel vom Ende der Periode aus.

Schätzwert bezieht sich auf die Höhe des zu berechnenden Zinssatzes.

„=Zahl!“ wird ausgegeben, wenn Excel keine Lösung innerhalb eines bestimmten Intervalls finden kann, d.h. der Zinssatz konvergiert nicht.

Dann sollte man einen anderen Schätzwert eingeben, wobei normalerweise Konvergenz bei einem Schätzwert zwischen 0 und 1 erreicht wird.

Wird kein Wert für Schätzwert eingegeben, geht Excel von 10% aus.

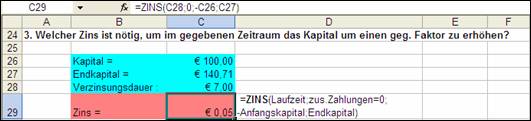
Abbildung 4: Ausschnitt aus dem Beispiel für Zinssatz

1.8 ZINSZ (IPMT)

ZINSZ gibt die Höhe der zu entrichtenden Zinsen für das Restkapital eines Kredites in einer bestimmten Periode aus.

=ZINSZ(Zins;Zr;Zzr;Bw;Zw;F) oder engl. =IPMT(rate;per;nper;pv;fv;type)

Zins bedeutet Zinssatz pro Periode. Die genaue Beschreibung dieses Argumentes ist unter Punkt 7 zu finden.

Zr bedeutet Zeitraum und gibt die Periode an, für die der Zinsbetrag berechnet werden soll. Zr kann nur einen Wert im Bereich zwischen 1 und Zzr annehmen.

Zzr ist die Anzahl der Zahlungszeiträume. Eine genaue Beschreibung ist unter Punkt 9 zu finden.

Bw ist der Barwert. Genaue Beschreibung: Siehe Punkt 3.

Zw ist der zukünftige Wert, in diesem Fall der Endwert. Wird für Zw nichts eingegeben, wird automatisch 0 angenommen. Näheres siehe Punkt 10.

F ist die Fälligkeit, Beschreibung siehe Punkt 7.

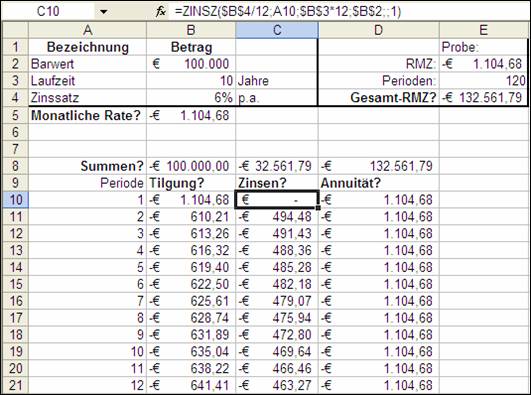
Abbildung 5: Ausschnitt aus dem Beispiel für ZINSZ

1.9 ZZR (NPER)

Mithilfe der Funktion ZZR (Zahlungszeiträume) kann die Anzahl der Zahlungsperioden einer Investition ermittelt werden, d.h. wie oft eine RMZ getätigt werden muss, um einem Endwert ZW zu erreichen.

=ZZR(Zins;Rmz;Bw;Zw;F) oder engl. =NPER(rate;pmt;pv;fv;type)

Zins ist der Zinssatz pro Periode. Eine genauere Beschreibung ist unter Punkt 7 zu finden.

Rmz ist die regelmäßige Zahlung. Die genaue Beschreibung dieses Arguments ist unter Punkt 11 zu finden.

Bw ist der Barwert. Genaue Beschreibung: Siehe Punkt 3.

Zw ist der zukünftige Wert, hier Endwert. Eine genaue Beschreibung dieses Argumentes ist unter Punkt 10 zu finden.

F ist die Fälligkeit. Für die genaue Beschreibung, siehe Punkt 7.

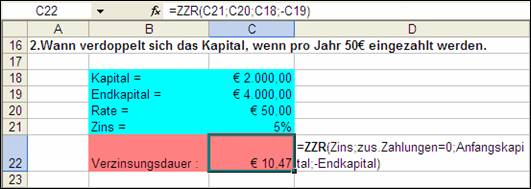
Abbildung 6: Ausschnitt aus dem Beispiel für Zählungszeiträume

1.10 ZW (FV)

ZW bedeutet zukünftiger Wert und gibt den Endwert einer Investition zurück.

=ZW(Zins;Zzr;Rmz;Bw;F) oder engl. =FV(rate;nper;pmt;pv;type)

Zins ist der Zinssatz pro Periode. Genau Beschreibung: Siehe Punkt 7.

Zzr ist die Anzahl der Zahlungszeiträume. Eine genaue Beschreibung ist unter Punkt 9 zu finden.

Rmz bedeutet regelmäßige Zahlung. Genaueres zu diesem Argument ist unter Punkt 11 zu finden.

Bw ist der Barwert. Die genaue Beschreibung dieses Argumentes findet sich unter Punkt 3.

F ist die Fälligkeit. Genaueres: Siehe Punkt 7.

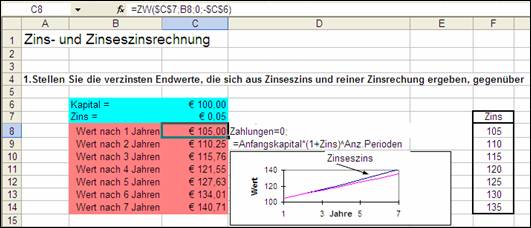
Abbildung 7: Ausschnitt aus dem Beispiel für zukünftiger Wert

1.11 RMZ (PMT)

Die Funktion Regelmäßige Zahlung liefert die Höhe eines regelmäßig zu entrichtenden Betrages, wobei jedoch ein konstanter Zinssatz und Zahlungen in jeweils derselben Höhe vorausgesetzt werden.

=RMZ(Zins;Zzr;Bw;Zw;F) oder engl. =PMT(rate;nper;pv;fv;type)

Zins ist der Zinssatz pro Periode. Näheres zu diesem Argument ist unter Punkt 7 zu finden.

Zzr ist die Anzahl der Zahlungszeiträume. Eine genauere Beschreibung ist unter Punkt 9 zu finden.

Bw ist Barwert. Die genauere Beschreibung dieses Argumentes ist unter Punkt 3 zu finden.

Zw ist der zukünftige Wert, hier Endwert. Genauere Beschreibung: Siehe Punkt 10.

F gibt die Fälligkeit an. Die genaue Beschreibung dieses Arguments ist unter Punkt 7 zu finden.

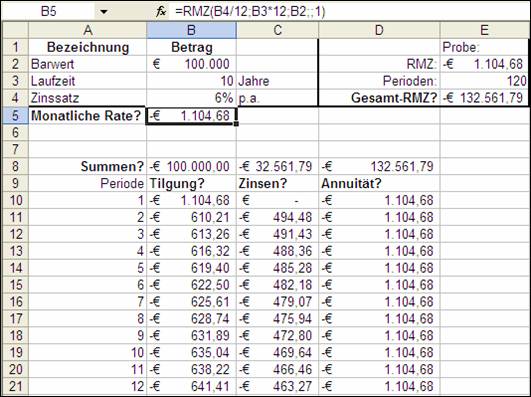
Abbildung 8: Ausschnitt aus dem Beispiel für regelmäßige Zahlung

2 Grundlagen der Datenanalyse

Trendlinien

Bekannt: Datenreihe der Vergangenheit

Unbekannt: Datenreihe der Zukunft

Trendlinien prognostizieren zukünftige Werte aufgrund existierender Datenwerte.

„Wie entwickelt sich der Umsatz in den nächsten Jahren?“

Datentabellen

Bekannt: Eine Variable oder zwei Variablen

Unbekannt: Ergebnis

Datentabellen zeigen das Ergebnis einer Formel, wenn Sie eine oder zwei Variablen dieser Formeln ändern.

„Wie hoch ist die jährliche Abschreibung des Computers, wenn die Laufzeit 3, 4 oder 5 Jahre beträgt und die Anschaffungskosten 2500 EUR oder 4300 EUR betragen?“

Zielwertsuche

Bekannt: Ergebnis

Unbekannt: Variable

Mit dieser Methode können Sie bestimmen, wie sich eine Variable einer Formel ändert, wenn Sie ein bestimmtes Ergebnis erhalten möchten.

„Wie lange muss der Sparvertrag bei einem Startkapital von 4000 EUR und einem Zinssatz von 8 % laufen, bis sich das Kapital verdoppelt hat?“

Solver-Berechnungen

Bekannt: Ergebnis

Unbekannt: Mehrere Variablen und Bedingungen

Der Solver zeigt, wie sich bei einem bestimmten Ergebnis mehrere Variablen unter bestimmten Bedingungen ändern können.

„Welchen Preis muss das Unternehmen ansetzen, um bei bestimmten gegebenen Kosten den Gewinn zu maximieren?“

Szenarien

Unbekannt: Variablen und Ergebnis

Szenarien zeigen die Auswirkung auf ein Ergebnis, wenn sich bestimmte Werte, die das Ergebnis beeinflussen, ändern.

„Wie viele Arbeitsstunden benötigt ein Projekt, wenn 10, 20, 30, … Mitarbeiter mit verschiedenen Arbeitsmitteln zur Verfügung stehen?“

3 Zielwertsuche

Bei der Zielwertsuche ist das Ergebnis (=Zielwert) bekannt und eine Variable (=Parameter), von der das Ergebnis abhängt, wird gesucht.

3.1 Vorgangsweise

1. Aufrufen über das Menü [Tools] – [Goal Seek] bzw. [Extras] – [Zielwertsuche]

2. Die einzelnen Parameter eingeben:

• In das Feld set cell bzw. Zielzelle den Bezug für die Zelle eingeben, die die Formel enthält, die aufgelöst werden soll.

• In das Feld To value bzw. Zielwert das gewünschte Ergebnis eingeben.

• In das Feld By changing cell bzw. Veränderbare Zelle den Zellbezug für die Zelle mit dem zu verändernden Wert eingeben.

3. OK klicken.

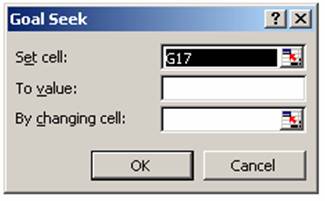
Abbildung 9: Zielwertsuche Parameter festlegen

Anschließend wird das Fenster Goal Seek Status bzw. Status der Zielwertsuche geöffnet.

Zu beachten:

• Die Zielzelle muss eine Formel enthalten.

• Die veränderbare Zelle muss einen Wert enthalten, da die Formel in der Zielzelle die Berechnung mit diesem Wert durchführt. Sie darf jedoch keine Formel enthalten.

3.2 Ergebnis der Zielwertsuche

Im Dialogfeld Goal Seek Status bzw. Status der Zielwertsuche sind Informationen über den Erfolg der Zielwertsuche sowie den gefundenen Wert angegeben.

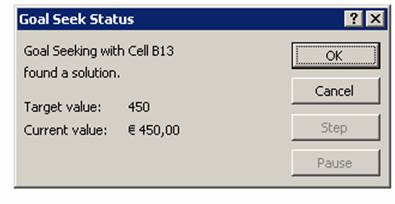
Abbildung 10: Ergebnis der Zielwertsuche

Weitere Optionen des Fensters Status der Zielwertsuche:

Pause

Mit der Schaltfläche Pause können Berechnungen angehalten werden. Danach wird daraus die Schaltfläche Weiter.

Step bzw. Schritt

Mit dieser Schaltfläche lassen sich mit Pause angehaltene Berechnungen schrittweise weiter ausführen.

Next bzw. Weiter

Mit der Schaltfläche Weiter können mit Pause angehaltene Berechnungen wieder gestartet werden.

4 Solver

Zum Unterschied zur Zielwertsuche können beim Solver mehrere Zellen variabel sein. Die Funktion des Solvers liegt darin, so lange die Werte in den veränderbaren Zellen anzupassen, bis er den Optimalwert findet. Folgende Elemente werden dazu benötigt:

• Zielzelle

• Veränderbare Zellen

• ev. Nebenbedingungen

Der Solver wird über das Menü [Tools] – [Solver] bzw. [Extras] – [Solver] aufgerufen. Es erscheint folgendes Bild:

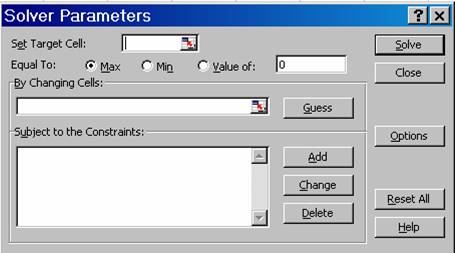
Abbildung 11: Solver Parameter

Im Folgendem werden die einzelnen Solver Parameter genauer erklärt.

4.1 Zielzelle

Diese Zelle soll durch Einsetzen unterschiedlicher Werte in die veränderbaren Zellen optimiert werden. Die Zielzelle muss immer eine Formel enthalten.

Zuerst wird die Zielzelle eingegeben bzw. die Zelle markiert. Anschließend wählt man eine der folgenden Optionen aus:

Max

Inhalt der Zielzelle soll durch Verändern der variablen Zellen maximiert werden (z.B. maximaler Gewinn)

Min

Inhalt der Zielzelle soll durch Verändern der variablen Zellen minimal werden (z.B. minimale Kosten)

Value of bzw. Wert

Hier kann man einen bestimmten Wert festlegen (z.B. 0)

4.2 Veränderbare Zellen

Diese Zellen werden vom Solver so lange verändert, bis alle Nebenbedingungen erfüllt sind und die Zielzelle den Zielwert erreicht hat. Die variablen Zellen müssen direkt oder indirekt mit der Zielzelle verbunden sein. Es können bis zu 200 veränderbare Zellen definiert werden.

Im Feld By changing cells bzw. Veränderbare Zellen sind die variablen Zellen einzugeben.

Bei Betätigung der Schaltfläche Guess bzw. Schätzen werden die veränderbaren Zellen automatisch festgelegt. Excel sucht nach allen formellosen Zellen, die in der Formel der Zielzelle verwendet werden.

4.2.1 Definition von Ausgangswerten

Bei der Lösung des Problems werden die Werte in Abhängigkeit von den Anfangswerten der veränderbaren Zellen berechnet.

Wenn der Solver eine Lösung für ein nichtlineares Problem gefunden hat, die erheblich von den Erwartungen abweicht, kann ein Versuch mit anderen Ausgangswerten für die veränderbaren Zellen hilfreich sein. Auch die Lösungszeit kann reduziert werden, indem die veränderbaren Zellen auf Werte gesetzt werden, die dem Optimum vermutlich sehr nahe kommen.

Bei linearen Modellen haben die Anfangswerte in den veränderbaren Zellen keinen Einfluss auf die Endwerte oder die Lösungszeit.

4.3 Nebenbedingungen

Für jede Zelle bzw. jeden Zellbereich können Bedingungen formuliert werden, die den Wert der Zelle genauer beschreiben. Diese Nebenbedingungen werden vom Solver bei der Lösung des Problems berücksichtigt. Bei nichtlinearen Problemen können bis zu 100 Nebenbedingungen festgelegt werden und bei aktiviertem Kontrollkästchen Assume Linear Model bzw. Lineares Modell voraussetzen im Dialogfeld Optionen ist die Anzahl der Nebenbedingungen unbegrenzt.

Durch Drücken der Schaltfläche Add kann eine Nebenbedingung hinzugefügt werden. Eine bestehende Bedingung wird mit Change verändert und mit Delete gelöscht.

Durch Betätigung der Schaltfläche Add erscheint folgendes Dialogfenster:

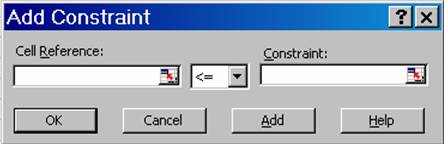
Abbildung 12: Solver: Nebenbedingung hinzufügen

Cell reference bzw. Zellbezug

Der Bezug der Zelle dessen Wert durch Nebenbedingungen eingegrenzt wird.

Constraint bzw. Nebenbedingung

Ein Wert, der zur Problemlösung erfüllt sein muss; es kann auch auf eine Zelle oder eine Formel verwiesen werden.

Folgende Beziehungen zwischen Bezugsquelle und Bedingung sind möglich:

<= Kleiner gleich

>= Größer gleich

= Gleich

Int/Ganzz. Ganzzahlig

Bin Binäre Zahl (0 oder 1)

Die Beziehungen int und bin können nur in Nebenbedingungen für veränderbare Zellen verwendet werden.

Um die Nebenbedingung zu bestätigen, muss die Schaltfläche OK gedrückt werden. Zu Eingabe weiterer Nebenbedingungen muss wiederum die Schaltfläche Add betätigt werden.

4.4 Einstellungen des Solvers

Durch Betätigung der Schaltfläche Optionen können Voreinstellungen des Solvers, Schnelligkeit und Genauigkeit der Berechnung beeinflusst werden.

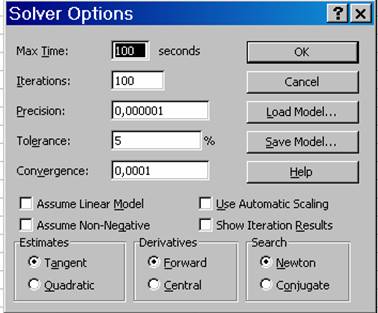
Abbildung 13: Solver Optionen

Max Time bzw. Höchstzeit

gibt die maximale Lösungszeit in Sekunden an. Es können höchstens 32.767 Sekunden (ca. 9 Stunden) eingegeben werden. Falls die maximale Zeit überschritten wird, bevor der Solver eine Lösung gefunden hat, erscheint folgendes Dialogfenster:

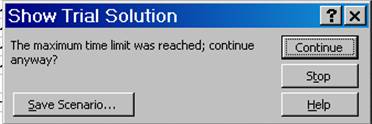
Abbildung 14: Solver Zwischenergebnis Höchstzeit

Hier hat man nun die Möglichkeit den Lösungsprozess zu stoppen. Über die Schaltfläche Continue bzw. Weiter wird der Rechenprozess fortgesetzt und die Zeitbeschränkung wird nicht mehr beachtet.

Iterations bzw. Iterationen

Damit wird die maximal zulässige Anzahl von Zwischenberechnungen beschränkt. Bei Überschreitung der Beschränkung zeigt sich folgendes Fenster:

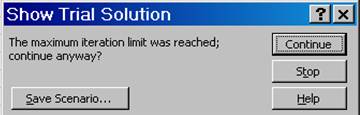
Abbildung 15: Solver Zwischenergebnis Iterationsgrenze

Precision bzw. Genauigkeit

Hier kann die Genauigkeit des Ergebnisses festgelegt werden. Die Zahl, die hier eingegeben wird, bestimmt, wie genau der Zellbezug mit der Bedingung übereinstimmen muss, damit die Nebenbedingung erfüllt ist. Je kleiner die Zahl ist, desto größer ist die Genauigkeit. Diese Zahl muss zwischen 0 und 1 liegen.

Tolerance bzw. Toleranz

Dieser Wert gibt die zulässige Fehlerabweichung in Prozent für Ganzzahlen an und wird verwendet, da manche Lösungsvorgänge (z.B. bei vielen Nebenbedingungen) sehr viel Zeit in Anspruch nehmen.

Convergence bzw. Konvergenz

Bei Unterschreitung der Zahl in diesem Feld durch die relative Änderung in der Zielzelle bei den letzten 5 Iterationen, hält der Solver an. Die Konvergenz kann nur bei nichtlinearen Problemen angewendet werden.

Assume Linear Model bzw. Lineares Modell voraussetzen

Bei Aktivierung des Kontrollkästchens wird ein lineares Modell vorausgesetzt. Dadurch wird der Lösungsvorgang beschleunigt, wenn alle Beziehungen im Modell linear sind und entweder ein lineares Optimierungsproblem gelöst oder ein linearer Näherungswert für ein nichtlineares Problem gesucht wird. Diese Option ist für das Lösen von Optimierungsaufgaben nicht unbedingt notwendig. Wenn man sich nicht sicher ist, dann sollte man dieses Kontrollkästchen nicht aktivieren. Auf diese Weise kann man ebenso lineare Optimierungsaufgaben lösen.

Assume Non-Negativ bzw. Nicht-Negativ voraussetzen

Der Solver nimmt hier einen unteren Grenzwert von Null an für die variablen Zellen, die keine Nebenbedingungen mit einem unteren Grenzwert haben.

Use Automatic Scaling bzw. Automatische Skalierung anwenden

Eine Einstellung, die verwendet werden soll, wenn die Werte der variablen Zellen von den Werten der Zielzelle stark abweichen, z.B. bei der Maximierung des prozentuellen Gewinns auf der Grundlage von Investitionen in Millionenhöhe.

Show Iteration Results bzw. Iterationsergebnisse anzeigen

Zeigt nach jeder Zwischenberechnung folgendes Fenster und das Ergebnis am Arbeitsblatt an:

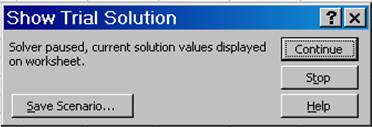
Abbildung 16: Solver Zwischenergebnis Iterationsergebnisse

Auch hier ist es wieder möglich den Solver bei seinen Berechnungen zu unterbrechen.

Estimates bzw. Schätzung

Diese Einstellung gibt den Lösungsansatz, der bei der Ermittlung der Schätzwerte der Grundvariablen bei jeder eindimensionalen Suche verwendet wird an.

· Tangent bzw. Linear: Verwendung der linearen Extrapolation

· Quadratic bzw. Quadratisch: Verwendung der quadratischen Extrapolation (führt unter Umständen bei extrem nichtlinearen Problemen zu verbesserten Ergebnissen)

Derivatives bzw. Differenz

· Forward bzw. Vorwärts: Der Punkt der vorhergehenden Iteration wird für die Berechnung des nächsten Punktes genutzt. Dadurch wird die Berechnungszeit verkürzt.

· Central bzw. Zentral: Die Berechnungszeit dauert hier länger, jedoch ist diese Form besser wenn sich die Differenzen der Iterationspunkte stark ändern.

Search bzw. Suchen

Diese Einstellung gibt den für die Iterationen verwendeten Algorithmus an, um die Suchrichtung festzulegen.

· Newton: Hier wird ein Quasi-Newton-Verfahren verwendet. Der Vorteil von diesem Verfahren ist, dass weniger Zwischenergebnisse benötigt werden, dafür aber mehr Arbeitsspeicher erforderlich ist.

· Conjugate bzw. Gradient: Bei diesem Verfahren wird weniger Arbeitsspeicher benötigt, jedoch ist im Allgemeinen eine größere Anzahl von Zwischenergebnissen notwendig, um eine bestimmte Genauigkeit zu erzielen. Diese Option ist dann sinnvoll, wenn das Problem umfangreich ist und der zur Verfügung stehende Speicherplatz eventuell nicht ausreicht.

Die Einstellungen Schätzung, Differenz und Suchen betreffen nur den Standard GRG Solver und verbessern den Lösungsprozess meist nur in wissenschaftlichen oder technischen Anwendungen. Für den Normalgebrauch ist es deshalb meist besser, diese Voreinstellungen des Solvers beizubehalten und eher die vorher genannten Optionen zu verändern (obwohl eine Änderung der Einstellungen Schätzung, Differenz und Suchen sicher keinen „Schaden“ anrichten wird).

4.5 Solver-Modelle verwalten

Das erste Solver-Modell wird durch Excel automatisch mit der Tabelle gespeichert. Durch die Schaltfläche Save Model bzw. Modell speichern in den Optionen können mehrere Modelle gesichert werden.

Die Zellbezüge der Zielzelle und der veränderbaren Zellen und auch die Nebenbedingungen können gespeichert werden, um sie zu einem späteren Zeitpunkt wieder zu verwenden.

Abbildung 17: Solver-Modell speichern

Hier wird der Tabellenbereich ausgewählt, in dem man das Modell speichern will.

Durch Betätigung der Schaltfläche Load Model bzw. Modell laden können diese Einstellungen für die aktuelle Tabelle angewendet werden.

4.6 Solver Parameter zurücksetzen

Die geänderten Solver-Einstellungen bleiben während der Arbeitssitzung von Excel erhalten. Bei einer neuen Problemlösung werden wieder automatisch die Standardeinstellungen herangezogen. Es ist aber auch möglich die ursprüngliche Einstellungen manuell wiederherzustellen durch Betätigung der Schaltfläche Reset All bzw. Zurücksetzen.

4.7 Das Ergebnis

Das Ergebnis wird in der Tabelle angezeigt und gleichzeitig wird folgendes Dialogfeld sichtbar:

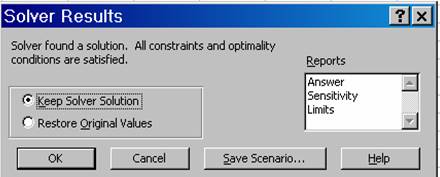
Abbildung 18: Solver Ergebnis

Keep Solver Solution

Hier wird die Lösung beibehalten.

Restore Original Values

Mit Anklicken dieses Optionsfeldes werden die Ausgangswerte wiederhergestellt.

4.7.1 Solver Vollzugsmeldungen

Hat der Solver eine Lösung gefunden, wird im Dialogfeld Solver Results bzw. Ergebnis eine der folgenden Meldungen angezeigt:

• Solver hat eine Lösung gefunden. Alle Nebenbedingungen und Optionen wurden eingehalten
Alle Nebenbedingungen wurden genau erfüllt. Für die Zielzelle wurde ein Höchst- oder Mindestwert gefunden.

• Solver hat die aktuelle Lösung durch Konvergieren erreicht. Alle Nebenbedingungen wurden eingehalten

Die relative Änderung in der Zielzelle liegt unter dem im Dialogfeld Optionen im Feld Konvergenz eingestellten Wert für die letzten fünf Zwischenergebnisse. Wenn Sie die Konvergenz auf einen kleineren Wert einstellen, kann Solver bei verlängerter Lösungszeit eine bessere Lösung ermitteln.

Wird keine optimale Lösung erzielt, zeigt Solver eine der folgenden Meldungen im Dialogfeld Ergebnis an:

• Solver kann die aktuelle Lösung nicht verbessern. Alle Nebenbedingungen wurden eingehalten

Obwohl nur eine annähernde Lösung gefunden wurde, können mit Hilfe des Iterationsprozesses keine besseren als die angezeigten Werte erreicht werden. Entweder kann keine höhere Genauigkeit erzielt werden oder die Genauigkeit ist zu niedrig eingestellt.

• Solver wurde beim Erreichen der Höchstzeit abgebrochen

In der maximal vorgesehenen Zeit wurde keine befriedigende Lösung gefunden.

• Solver wurde beim Erreichen der Iterationsgrenze abgebrochen

Mit der maximal zulässigen Anzahl von Iterationen wurde keine befriedigende Lösung gefunden.

• Werte der Zielzellen konvergieren nicht

Der Wert der Zielzelle wächst oder fällt gegen Unendlich, obwohl alle Nebenbedingen erfüllt sind.

• Solver konnte keine realisierbare Lösung finden

Solver konnte kein Zwischenergebnis ermitteln, das alle Nebenbedingungen im Rahmen der angegebenen Genauigkeit erfüllt. Die Nebenbedingungen sind vermutlich unvereinbar.

• Solver wurde auf Veranlassung des Anwenders unterbrochen

Im Dialogfeld Zwischenergebnis wurde nach dem Unterbrechen des Lösungsprozesses oder beim schrittweisen Anzeigen der Zwischenergebnisse auf Stopp geklickt.

• Die Linearitätsbedingung wurde nicht eingehalten

Das Kontrollkästchen Lineares Modell voraussetzen wurde aktiviert, aber die letzte Berechnung ergibt Werte, die mit dem linearen Modell nicht übereinstimmt.

• Solver hat in einer Zielzelle oder in einer Nebenbedingung einen Fehlerwert gefunden.

Eine oder mehrere Formeln haben bei der letzten Berechnung einen Fehlerwert ergeben. In der fehlerhaften Ziel- oder Nebenbedingungszelle muss die betreffende Formel geändert werden, um einen brauchbaren numerischen Wert zu erhalten.

• Es ist nicht genügend Speicherplatz zur Lösung des Problems vorhanden.

Microsoft Excel konnte Solver den erforderlichen Arbeitsspeicher nicht zuteilen. Man sollte einige Dateien oder Anwendungen schließen und den Vorgang erneut durchführen.

• Eine andere Microsoft Excel-Instanz verwendet bereits SOLVER.DLL.

Mehrere Microsoft Excel-Sitzungen werden gleichzeitig ausgeführt und die Datei SOLVER.DLL wird bereits in einer anderen Sitzung verwendet.

4.7.2 Berichte erstellen

Im Listenfeld Reports bzw. Berichte können folgende Einträge gewählt werden:

Answer bzw. Antwort

Der Bericht listet die Zielzelle und die veränderbaren Zellen mit den Ausgangswerten und Endergebnissen und den Nebenbedingungen auf. Man kann genau erkennen, ob eine Nebenbedingung die Lösung eingeschränkt hat. Die Differenz gibt einen Wert zwischen dem Lösungswert und der oberen bzw. unteren Grenze, die von dieser Nebenbedingung vorgegeben ist, an. Eine einschränkende Nebenbedingung, die optimal angeglichen werden konnte, hat den Differenzwert 0.

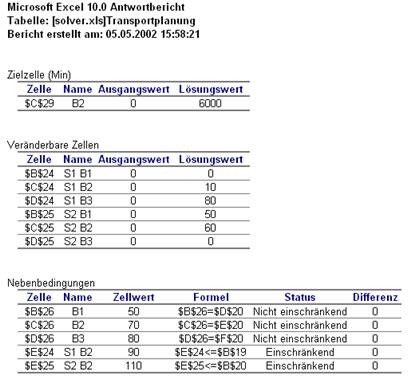
Abbildung 19: Solver Antwortbericht

Anmerkung: Für den Eintrag in der Spalte Name wählt der Solver die erste Textzelle links und die erste Textzelle oberhalb der Zelle aus, auf die er Bezug nimmt.

Sensitivity bzw. Empfindlichkeit

Dieser Bericht liefert Informationen darüber, wie empfindlich die Lösung auf kleine Änderungen in der angegebenen Formel im Feld Zielzelle oder in den Nebenbedingungen reagiert. Zusätzlich werden statistische Berechnungen vorgenommen.

Limits bzw. Grenzwert

In diesem Bericht werden alle oberen und unteren Grenzwerten sowie die Auswirkung auf die Zielzelle angezeigt. Der untere Grenzwert entspricht dem kleinsten Wert, den die veränderbare Zelle annehmen kann, während die Werte aller anderen veränderbaren Zellen beibehalten und die Nebenbedingungen erfüllt werden. Der obere Grenzwert ist der größte Wert.

4.7.3 Szenario speichern

Mit Klick auf die Schaltfläche Szenario speichern, erscheint das gleichnamige Dialogfeld. Damit können die veränderbaren Zellwerte als Szenario gespeichert werden. Anschließend im Feld Szenarioname den Namen des Szenarios eingeben.

Genaueres zu Szenarien im Kapitel 3.

Abbildung 20: Solver Szenario speichern

5 Szenario-Manager

Szenarien ermöglichen das Ersetzen einer Reihe von Werten durch andere Werte, um die unterschiedlichen Ergebnisse vergleichen und beurteilen zu können. Es können pro Szenario 32 veränderbare Zellen eingegeben werden.

5.1 Erstellen eines Szenarios

1. Aufrufen über das Menü [Tools] – [Scenarios] bzw. [Extras] – [Szenarien].

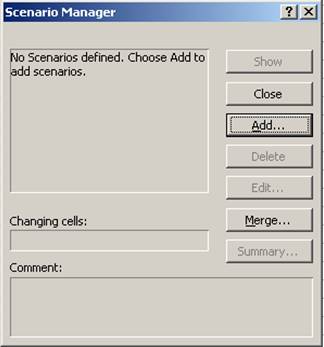
Abbildung 21: Szenariomanager starten

2. Auf Hinzufügen klicken.

3. In das Feld Szenarienname einen Namen für das Szenario eingeben.

4. In das Feld Veränderbare Zellen die zu ändernden Zellbezüge eingeben.

5. Unter Schutz die gewünschten Optionen auswählen.

6. Anschließend auf OK klicken.

7. Eventuell einen Kommentar schreiben, um die Werte auch zu einem späteren Zeitpunkt noch nachvollziehen zu können.

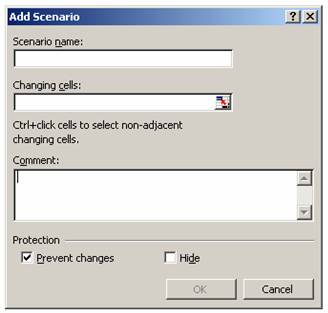
Abbildung 22: Neues Szenario hinzufügen

8. Im Dialogfeld Szenariowerte die Werte für die veränderbaren Zellen eingeben.

9. Auf OK klicken, um das Szenario zu erstellen.

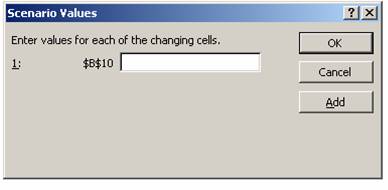
Abbildung 23: Szenariowerte eingeben

10. Sollen zusätzliche Szenarien erstellt werden, Schritt 2-8 wiederholen. Wenn alle gewünschten Szenarien erstellt wurden, auf OK und anschließend im Dialogfeld Szenarien auf Schließen klicken.

5.2 Szenarien schützen

Damit Szenarien geschützt werden können, muss das Tabellenblatt geschützt sein. Dazu müssen folgende Voreinstellungen vorgenommen werden.

1. Aufrufen über das Menü [Tools] – [Protection] – [Protect Sheet] bzw. [Extras] – [Schutz] – [Blatt schützen]

2. Kennwort eingeben

3. Das Kontrollfeld Scenarios bzw. Szenarios bearbeiten aktivieren.

Unter dieser Voraussetzung kann das Szenario mit den folgenden Kontrollfeldern vor unberechtigtem Zugriff geschützt werden:

Prevent Changes

Andere Benutzer können nicht auf das Szenario zugreifen.

Hide

Der Name im Listenfeld Szenarien wird ausgeblendet. Damit kann das Szenario nicht ausgewählt werden.

5.3 Anzeigen eines Szenarios

1. Im Menü [Tools] auf [Scenario] bzw. [Extras] auf [Szenarien] klicken

2. Auf den Namen des gewünschten Szenarios klicken.

3. Auf Anzeigen klicken, um das Szenario anzuzeigen. Die aktuellen Werte der veränderbaren Zellen werden durch die Werte des Szenarios ersetzt.

5.4 Bearbeiten eines Szenarios

1. Im Menü Menü [Tools] – [Scenario] bzw. [Extras] – [Szenarien] klicken.

2. Auf den Namen des zu bearbeitenden Szenarios und dann auf Edit bzw. Bearbeiten klicken.

3. Die gewünschten Änderungen durchführen.

4. OK klicken, um die Werte im ursprünglichen Szenario durch die neuen Werte zu ersetzen.

5.5 Szenarien zusammenführen

1. Die Arbeitsmappen öffnen, die Szenarien enthalten, die zusammengeführt werden sollen.

2. In das Arbeitsblatt wechseln, in das die Szenarien zusammengeführt werden sollen.

3. Im Menü [Tools] auf [Scenario] bzw. [Extras] auf [Szenarien] klicken.

4. Auf die Schaltfläche Merge bzw. Zusammenführen klicken.

5. Im Listenfeld Book bzw. Mappe die Datei auswählen, die das Tabellenblatt enthält, aus dem die Szenarien dem aktuellen Tabellenblatt hinzugefügt werden sollen.

6. Im Listenfeld Sheet bzw. Blatt das gewünschte Tabellenblatt auswählen.

7. Den Vorgang wiederholen, wenn Szenarien aus weiteren Arbeitsblättern zusammengeführt werden sollen.

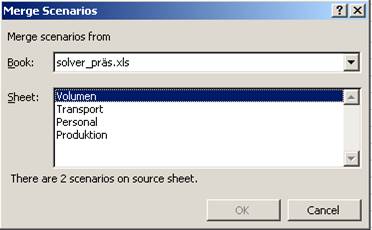
Abbildung 24: Szenario zusammenführen

5.6 Erstellen eines Szenarioberichtes

In einem Übersichtsbericht können die ersten 251 Szenarien angezeigt werden.

1. Im Menü Menü [Tools] auf [Scenario] bzw. [Extras] auf [Szenarien] klicken.

2. Auf Zusammenfassung klicken.

3. Durch Aktivieren des Optionsfeldes Szenariobericht bzw. Szenario-Pivot-Table-Bericht den Berichtstyp auswählen.

4. In das Feld Result cells bzw. Ergebniszellen die Zellbezüge eingeben, die auf Zellen verweisen, deren Werte durch die Szenarien verändert wurden. Mehrere Bezüge müssen durch Semikolon getrennt werden.

5. OK klicken und der Szenariobericht wird auf einem neuen Tabellenblatt erstellt.

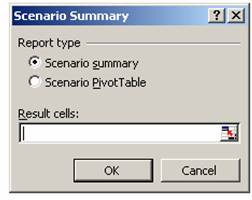
Abbildung 25: Szenariobericht erstellen

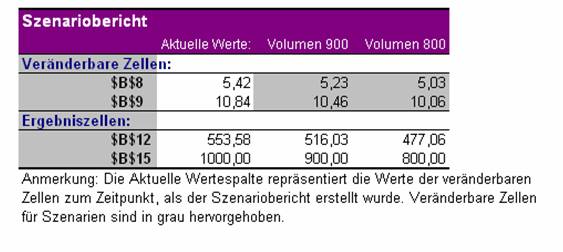
Abbildung 26: Szenariobericht

6 Makros in Microsoft Excel

6.1 Einführung:

Makros haben die Aufgabe häufig verwendete Arbeitsschritte automatisch auszuführen. Dies funktioniert indem die einzelnen Schritte zuerst aufgezeichnet und gespeichert werden und dann zu einem späteren Zeitpunkt automatisch ausgeführt werden und so dem Anwender viel Zeit ersparen können.

Prinzipiell können mit Makros alle beliebigen Aktionen automatisiert werden. Mögliche Einsatzgebiete könnten zum Beispiel sein:

· Formatieren von Zellen

· Automatisches Erstellen von Diagrammen

· Sortieren von Zellen

6.2 Schema der Makroaufzeichnung:

Das Aufzeichnen von Makros läuft immer in drei Schritten ab. Zuerst wird die Aufzeichnung gestartet, dann werden die einzelnen, zu automatisierenden Arbeitsschritte ausgeführt und zum Schluss wird die Aufzeichnung beendet.

Um keine unnötigen Schritte im Makro abzuspeichern, sollte man sich vorher ein Konzept überlegen, nach dem man vorgeht.

Abbildung 27: Schema der Aufzeichnung

6.3 Aufzeichnung:

6.3.1 Starten des Makrorecorders:

Der Makrorecorder befindet sich im Menü Extras- Makro- Makro aufzeichnen

Man hat hier die Möglichkeit vor der Aufzeichnung dem Makro einen Namen und eine Tastenkombination zuzuweisen. Ebenfalls kann eine kurze Beschreibung des Makros angegeben werden (als Standard steht hier das Datum und der Name des Erstellers). All diese Informationen können auch noch nachträglich abgeändert werden.

Abbildung 28: Starten der Aufzeichnung

6.3.2 Aufzeichnen der Arbeitsschritte:

Der nächste Schritt ist nun die Aufzeichnung der einzelnen Arbeitsschritte. Das erscheinende Fenster( Abbildung 29: Aufzeichnung beenden) zeigt an, dass sich Excel nun im Aufnahmemodus befindet. Alle Schritte die nun ausgeführt werden, werden aufgezeichnet. Sollte es passieren, dass ein nicht beabsichtigter Arbeitsschritt getätigt wird, kann dieser wieder mit dem Rückgängig- Button aus der Aufzeichnung entfernt werden.

Abbildung 29: Aufzeichnung beenden

Der Button neben dem Stopp- Button gibt an ob ein absoluter oder relativer Bezug verwendet wird

Der relative Bezug ist vom Programm als Standard definiert, und wird auch in den meisten Fällen benötigt. Das Makro bezieht sich dann immer auf die Zelle, die beim Ausführen aktiv ist.

Beim absoluten Bezug bezieht sich Excel immer auf die Zelle die während der Aufzeichnung aktiviert war.

6.3.3 Beenden der Aufzeichnung:

Hat man alle gewünschten Schritte ausgeführt wird die Aufzeichnung mit dem Stopp- Button beendet.

6.4 Ausführen des Makros:

Man hat nun die Möglichkeit das aufgezeichnete Makro auf unterschiedliche Arten zu starten.

· Die erste Möglichkeit ist, das Makro manuell zu starten. Dies geschieht im Menü Extras- Makro-Makros. Hier wählt man nun das gewünschte Makro aus und startet es durch den Button: Ausführen.

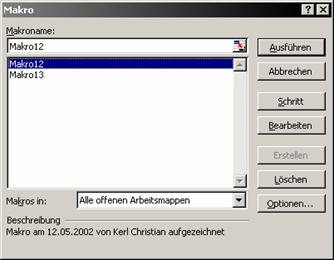
Abbildung 31: Ausführen und Bearbeiten eines Makros

· Das Makro kann ebenfalls durch die zugewiesene Tastenkombination ausgeführt werden.

Eine weitere Möglichkeit, das Makro zu starten, ist, direkt in der Arbeitsmappe einen Button zu installieren.

Abbildung 32: Die "Steuerelement-Toolbox" Leiste

Dazu aktiviert man die Symbolleiste "Steuerelement-Toolbox" und wählt das Symbol "Befehlsschaltfläche".
Mit der Maus wird dann direkt im Arbeitsblatt eine Befehlsschaltfläche aufgezogen. Im Kontextmenü dieser Befehlsschaltfläche kann man unter "Code anzeigen" den Visual Basic Code für die Schaltfläche eingeben und bearbeiten.

Man kann auch einer importierten Grafik ein Makro zuweisen, indem man es mit der rechten Maustaste anklickt, und dann „Makro zuweisen“ auswählt.

· Die letzte Möglichkeit ein Makro zu aktivieren ist, dass man dem Makro in der Symbolleiste ein Symbol zuordnet.
Dies geschieht unter dem Menüpunkt EXTRAS-ANPASSEN, wo sich unter dem Menüblatt "Befehle" auch der Punkt "Makros" befindet.
Nun zieht man entweder den Befehl "Schaltfläche anpassen" in eine der Symbolleisten. Um nun ein Makro zuzuweisen, klickt man mit der rechten Maustaste auf die neue Schaltfläche und weist im darauf folgenden Menü ein Makro zu.
Unter EXTRAS-ANPASSEN-AUSWAHL ÄNDERN kann man der neuen Schaltfläche einen benutzerdefinierten Namen geben oder ihr ein neues Symbol zuweisen, beziehungsweise selbst eines entwerfen.
Alternativ lässt sich auf die selbe Weise ein benutzerdefiniertes Menüelement in die Symbolleisten einbauen.

6.5 Visual Basic:

Die Aufzeichnung der Makros erfolgt durch die Microsoft-Office Programmiersprache Visual Basic. Die einzelnen, vom Benutzer gesetzten Arbeitsschritte werden als Anweisungen in Visual Basic verarbeitet. Excel kreiert automatisch den dazupassenden Code.

Der Visual Basic Code ist mittels dem in Excel enthaltenen Visual Basic Editor jederzeit bearbeitbar und veränderbar.

Es ist daher auch möglich, Makros ohne den Recorder zu erzeugen, allerdings ist dafür Kenntnis von Visual Basic und auch von den Parametern von Excel nötig

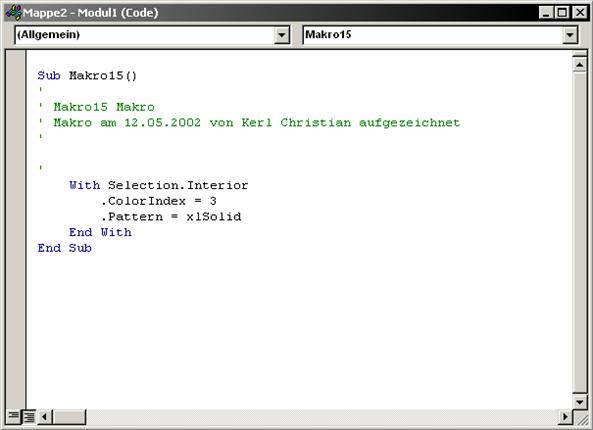
Abbildung 33: Visual Basic Editor

Mittels EXTRA-MAKRO-MAKROS und der Schaltfläche "Bearbeiten" kommt man direkt zum Visual Basic Code des Makros.

Dieser enthält:

· Einige Zeilen an Kommentar, die die Funktion des Makros beschreiben

· "Sub" und "End Sub", um Anfang und Ende des Makros zu kennzeichnen

· Sowie dem Namen des Makros

Aufgezeichnete Makros werden in Module gespeichert, wird die Arbeitsmappe zwischendurch geschlossen, wird ein neues Modul angelegt. Module können auch anderen Arbeitsmappen zur Verfügung gestellt werden.

6.6 Makroviren:

Da man mit Makros eigentlich jede Aktion automatisieren kann besteht auch die Möglichkeit Makros zu erzeugen, die bei der Ausführung Daten manipulieren oder auch löschen. Um sich davor zu schützen, dass solche Makros aktiv werden, prüft Excel beim Laden jedes gespeicherten Arbeitsblattes ob Makros vorhanden sind und fragt den Anwender ob diese sicherheitshalber deaktiviert werden sollen.

6.7 Quellenverzeichnis:

Microsoft Excel für Windows Automatisierung und Programmierung, Herdt Verlag, 2000

7 Matrizenrechnung in Excel

7.1 Mathematische Grundlagen

7.1.1 Definition

Eine Matrix ist ein rechteckiges Schema von n * m Elementen, die in m Zeilen und n Spalten angeordnet sind.

7.1.2 Praktische Beispiele

7.1.2.1 Quadratische Matrizen

Eine Matrix, bei der die Zeilenzahl gleich der Spaltenanzahl ist, heißt quadratische Matrix.

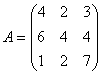
7.1.2.2 Nullmatrizen

Eine Matrix, in der alle Elemente null sind, nennt man Nullmatrix.

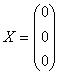
7.1.2.3 Gleichartige Matrizen

Zwei Matrizen sind genau dann gleichartig, wenn sie in Zeilen- und Spaltenanzahl übereinstimmen.

7.1.2.4 Gleiche Matrizen

Zwei Matrizen sind dann gleich, wenn sie gleichartig sind und in den entsprechenden Elementen übereinstimmen.

7.1.2.5 Transponierte Matrizen

Zwei Matrizen sind genau dann zueinander transponiert (oder gespiegelt), wenn jeweils eine Matrix dadurch entsteht, dass bei der anderen Matrix die Zeilen mit den Spalten vertauscht werden.

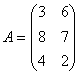
7.1.2.6 Diagonalmatrizen

Eine quadratische Matrix, bei der alle Elemente „außerhalb“ der Hauptdiagonale null sind, heißt Diagonalmatrix.

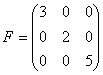
Die Hauptdiagonale einer Matrix ist die längste, von links oben nach rechts unten verlaufende Diagonale der Matrix.

7.1.2.7 Einheitsmatrizen

Eine quadratische Matrix, bei der alle Elemente die auf der Hauptdiagonale liegen, 1 sind (und alle anderen Elemente 0 sind!), bezeichnet man als Einheitsmatrix.

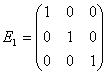
7.1.2.8 Symmetrische Matrizen

Eine quadratische Matrix, die ihrer transponierten Matrix gleich ist, heißt symmetrische Matrix.

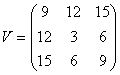
7.1.3 Rechnen mit Matrizen

7.1.3.1 Addition und Subtraktion von Matrizen

Ungleichartige Matrizen können nicht addiert werden. Gleichartige Matrizen werden addiert, indem man jedes Element der Matrix mit der entsprechenden Zahl der anderen Matrix addiert wird.

7.1.3.2 Multiplikation einer Matrix mit einer Zahl

Eine Matrix wird mit einer Zahl multipliziert, indem man jedes Element der Matrix mit der Zahl multipliziert.

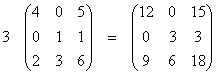
7.1.3.3 Multiplikation von Matrizen

Um zwei Matrizen miteinander multiplizieren zu können, muss die Spaltenanzahl der ersten Matrix gleich der Zeilenanzahl der zweiten Matrix sein.

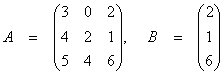
*A B**			2
			1
			6
3	0	2	18
4	2	1	16
5	4	6	50

7.1.3.4 Inverse Matrix (Kehrmatrix)

Die inverse Matrix A^-1 ist jene Matrix, mit der die ursprüngliche Matrix A von rechts oder von links multipliziert, die Einheitsmatrix liefert.

7.2 Matrizen in Excel

Mit Matrixformeln können mehrere Berechnungen gleichzeitig durchgeführt werden. Sie liefern je nach Anwendung entweder ein Ergebnis in einer Zelle oder unterschiedliche Ergebnisse in mehreren Zellen. Dabei greifen diese Formeln auf einen Zellenbereich (Matrix) zu. Matrixformeln erleichtern das Erstellen von gleichen Formeln für unterschiedliche Zellen und reduzieren fehlerhafte Eingaben. Um alle Formeln zu ändern, braucht der Anwender nur eine der Zellen mit Matrixformeln zu bearbeiten und wieder als Matrixformel einzugeben.

7.2.1 Syntax von Matrixformeln

§ Matrixformeln sind an den geschweiften Klammern zu Beginn und am Ende der Formel zu erkennen.

§ Innerhalb der geschweiften Klammern steht die gewünschte Berechnung bzw. Funktion, deren Syntax einer einfachen Formel entspricht.

§ Enthält die Matrixformel Argumente, die sich auf Matrixbereiche beziehen, müssen die Bezüge den gesamten Matrixbereich betreffen.

7.2.2 Matrizen erstellen und bearbeiten

(1) Markieren der Zelle, die das Ergebnis der Matrixformel beinhalten soll. Sollen verschiedene Ergebnisse in mehreren Zellen angezeigt werden, muss der Bereich der Ergebniszellen markiert sein.

(2) Eingeben der gewünschten Formel als einfache Formel, d.h. ohne geschweifte Klammern. Dabei muss sich die Formel auf die Matrix beziehen.

(3) Schließen der Eingabe mit der Tastenkombination STRG + Umschalten + Return

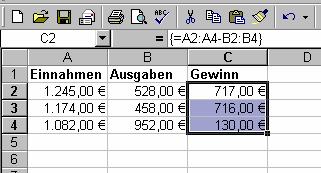
Abbildung 34: Eingabe einer einfachen Matrixformel

Excel erkennt die Formel als Matrixformel und setzt sie automatisch in geschweifte Klammern. Die Formeln werden in jede Zelle des zuvor markierten Bereichs eingefügt.

Man kann mit Matrizen NICHT ...

einzelne Zellen löschen oder verschieben

§ Zellen in einen Matrixbereich einfügen.

Man kann mit Matrizen ...

Zellinhalte einzelner Zellen ändern
einzelne Zellen kopieren und an anderer Stelle einfügen
einzelne Zellen formatieren
Matrixbereiche in konstante Werte umwandeln, um sie danach zu bearbeiten.

7.2.3 Matrizen markieren

Um die Matrixformel zu bearbeiten, muss der Anwender den Bereich mit den Ergebniszellen vorher markieren. In umfangreichen Tabellen ist dieser Bereich oft schwer zu finden. Als Alternative zum Markieren mit der Maus kann man den Bereich über das Dialogfenster INHALTE AUSWÄHLEN markieren.

Markieren einer beliebigen Zelle des Ergebnisbereiches.

Aufrufen des Menüpunktes BEARBEITEN – GEHE ZU (Alternative: STRG + G od. F5)

Betätigen der Schaltfläche INHALTE.

Im Dialogfenster INHALTE AUSWÄHLEN das Kontrollfeld AKTUELLES ARRAY aktivieren.

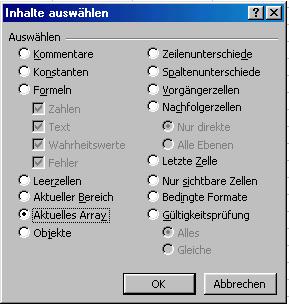
Abbildung 35: Matrixbereiche markieren

7.2.4 Matrixformel bearbeiten

(1) Markieren der Matrix mit den Ergebniszellen oder einer einzelnen Zelle der Matrix.

(2) Bearbeiten der Matrixformel, bzw. Neueingabe.

(3) Abschließen der Bearbeitung mit der Tastenkombination STRG + Umschalten + Return.

7.2.5 Matrix löschen

(1) Markieren der gesamten Matrix.

(2) Taste ENTF betätigen.

7.2.6 Ergebnisse der Matrix in konstante Werte umwandeln

(1) Markieren der Matrix, d.h. aller Zellen, die Matrixformeln beinhalten.

(2) Kopieren des Inhaltes der Zellen in die Zwischenablage.

(3) Aufrufen des Menüpunktes BEARBEITEN – INHALTE EINFÜGEN.

(4) Innerhalb der Optionsgruppe EINFÜGEN das Optionsfeld WERTE aktivieren und mit OK bestätigen.

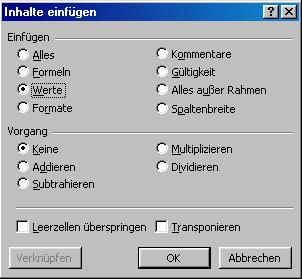
Abbildung 36: Umwandeln der Matrix in konstante Werte

Die Formeln werden an der gleichen Stelle mit den konstanten Werten überschrieben.

7.3 Matrixfunktionen

Excel kennt eine Vielzahl von Funktionen, die speziell zum Bearbeiten von Matrizen geeignet sind. Diese Funktionen können mit dem Funktionsassistenten erstellt werden. Die Matrixfunktionen lassen sich nach der Art der Ergebnisse kategorisieren. Anders als Datenbankfunktionen stellen Matrixfunktionen keine einheitliche Syntax dar. Die Argumente sowie deren Reihenfolge, die für die verschiedenen Funktionen notwendig sind, werden im Hilfesystem von Excel ausführlich beschrieben.

7.3.1 SVERWEIS

=VLOOKUP(lookup_value;table_array;col_index_num;true/false)

=SVERWEIS(Suchkriterium;Matrix;Spaltenindex;Bereich_Verweis)

Mit Hilfe des SVerweises ist es möglich, in einer Matrix einen bestimmten Wert auszugeben. Excel beginnt an der linken oberen Zelle der Matrix und sucht nach dem Kriterium in der ersten Spalte. Ist dieser Wert gefunden, geht Excel in die angegebene Spaltennummer der Matrix und gibt den dort enthaltenen Wert in der Zielzelle aus.

Der letzte Wert in der Formel heißt Wahr oder Falsch. Falsch bedeutet, dass das angegebene Suchkriterium genau gefunden werden muss. Wahr bedeutet, dass die Werte in der Matrix aufsteigend sortiert sind und ein Wert gefunden werden soll, der dem Suchkriterium am nächsten ist.

7.3.2 WVERWEIS

=HLOOKUP(lookup_value;table_array;row_index_num;...)

=WVERWEIS(Suchkriterium;Matrix;Zeilenindex;Bereich_Verweis)

Der Unterschied zum SVerweis besteht darin, dass Excel beim WVerweis das Kriterium in der ersten Zeile sucht und dann in der gefundenen Spalte in die Zeile der Matrix geht, die in der Formel angegeben ist.

7.3.3 MTRANS

=TRANSPOSE(array)

=MTRANS(Matrix)

Liefert die transponierte Matrix der angegebenen Matrix. MTRANS muss als Matrixformel in einem Bereich eingegeben werden, der so viele Zeilen und Spalten hat wie die ursprüngliche Matrix Spalten und Zeilen. Mit MTRANS werden die Zeilen und Spalten einer Matrix vertauscht. Der Anwender kann insbesondere einen horizontalen Vektor in einen vertikalen Vektor und umgekehrt überführen.

7.3.4 MINV

=MINV(array)

=MINV(Matrix)

Liefert die Inverse einer Matrix (die zur Matrix gehörende Kehrmatrix).

§ Wenn Zellen in der Matrix leer sind oder Text enthalten, gibt MINV den Fehlerwert #Wert! Zurück.

§ MINV gibt außerdem den Fehlerwert #Wert zurück, wenn die Anzahl der Zeilen und Spalten der Matrix nicht gleich ist.

§ Inverse Matrizen werden im Allgemeinen zur Lösung von Gleichungssystemen mit mehreren Variablen verwendet. Das Produkt einer Matrix und ihrer Inverse ist die Identitätsmatrix, eine quadratische Matrix, in der die Elemente auf der Hauptdiagonale gleich 1 und alle anderen Elemente gleich 0 sind.

7.3.5 MMULT

=MMULT(array1;array2)

=MMULT(Matrix1;Matrix2)

§ Matrix1;Matrix2 sind die Matrizen, die multipliziert werden sollen.

§ Die Anzahl der Spalten von Matrix1 muss mit der Anzahl der Zeilen von Matrix2 übereinstimmen, beide Matrizen dürfen nur Zahlen enthalten.

§ Matrix1 und Matrix2 können als Zellbereiche, Matrix-Konstanten oder Bezüge gegeben sein.

§ Gibt es Zellen, die leer sind oder Test enthalten, oder ist die Spaltenanzahl von Matrix1 nicht gleich der Zeilenanzahl von Matrix2, liefert MMULT den Fehlerwert #WERT!.

7.3.6 SUMMENPRODUKT

=SUMPRODUCT(array1;array2;...)

=SUMMENPRODUKT(Matrix1;Matrix2;…)

§ Matrix1; Matrix2; … sind 2 bis 30 Matrizen, deren Komponenten zunächst multipliziert und anschließend addiert werden sollen.

§ Die als Argumente angegebenen Matrizen müssen bezüglich der Zeilen- und Spaltenanzahl identisch sein. Ist dies nicht der Fall, liefert SUMMENPRODUKT den Fehlerwert #WERT!.

§ Matrixelemente, die keine numerischen Ausdrücke sind, behandelt SUMMENPRODUKT so, als wären sie mit 0 belegt.

8 Komplexe Zahlen

8.1 Einführung

8.1.1 Von den ganzen Zahlen zu den komplexen Zahlen

Wenn man nur mit ganzen Zahlen (...,-2,-1,0,1,2,...) rechnet, stößt man bald auf ein Problem: Man kann zwar Gleichungen wie 4x = 20 lösen (die Lösung wäre x = 5), doch bei 4x = 3 ist das nicht mehr so einfach, denn diese Gleichung hat in den ganzen Zahlen keine Lösung.

Damit solche Gleichungen lösbar werden, muss man eine neue Art von Zahlen einführen, die Bruchzahlen. Daher definiert man: ¾ ist die Zahl, welche die Gleichung 4x = 3 löst.

Bruchzahlen und ganze Zahlen zusammen nennt man rationale Zahlen.

Doch auch mit den rationalen Zahlen gibt es noch Probleme. Man kann zwar die Gleichung x² = 4 lösen (Lösung ist x = 2), aber x² = 2 hat in den rationalen Zahlen keine Lösung. Also müssen wieder neue Zahlen her: die irrationalen Zahlen. Und man definiert wieder: "die Wurzel aus 2" ist die Zahl, welche die Gleichung x² = 2 löst.
Irrationale und rationale Zahlen zusammen nennt man reelle Zahlen.

Aber jetzt kommt gleich das nächste Problem: die Gleichung x² = 2 kann man jetzt zwar lösen, aber die Gleichung x² = -1 hat immer noch keine Lösung. Es werden erneut neue Zahlen benötigt. Zu diesem Zweck führte Leonhard Euler die imaginäre Zahl i ein. Sie ist definiert als Lösung der Gleichung x² = -1.
Imaginäre und reelle Zahlen zusammen nennt man komplexe Zahlen.

8.1.2 Praktische Anwendungen

Ø Moderne Zahlenforschung

Ø Chaostheorie und Fraktalgeometrie

Ø Elektrotechnik

8.2 Definition von komplexen Zahlen

8.2.1 Imaginäre Zahlen

Die imaginären Zahlen sind Vielfache der sogenannten imaginären Einheit i, wobei i definiert ist durch:

i² = -1 bzw. i =

Eine imaginäre Zahl hat also die Form z = ai mit a Î R

8.2.2 Komplexe Zahlen und die Normalform

Eine komplexe Zahl z setzt sich aus einem Realteil Re(z) und einem Imaginärteil Im(z) zusammen.

z = a + ib wobei a und b reelle Zahlen sind.

a...der Realteil

ib...der Imaginärteil von z

Diese Form der Darstellung heißt Normalform einer komplexen Zahl.

Ist z₁ = a – ib so heißt z₁ die konjugiert komplexe Zahl zu z.

Die Menge der komplexen Zahlen wird durch den Großbuchstaben C abgekürzt.

8.2.3 Kartesische Darstellung komplexer Zahlen

Figure 1: Zahlenstrahl für reelle Zahlen

Bei komplexen Zahlen reicht ein Zahlenstrahl nicht mehr aus, man benötigt jetzt eine Zahlenebene. Um komplexe Zahlen in einem Koordinatensystem darstellen zu können, bedient man sich der Methode von Carl Friedrich Gauß (1777-1855).

Auf der x-Achse trägt man den Realteil und auf der y-Achse den Imaginärteil der komplexen Zahl auf.

Dadurch ergibt sich folgende Vektordarstellung einer komplexen Zahl z:

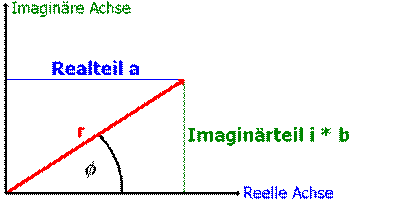
Figure 2: Gauß'sche Zahlenebene

Da die y-Achse nun nicht mehr aus reellen Zahlen besteht, sondern eben aus komplexen Zahlen, nennt man das zugehörige „komplexe“ Achsenkreuz auch die komplexe Ebene oder die Gauß’sche Zahlenebene.

Durch diese neue Form der Darstellung ergibt sich eine weitere Beschreibungsmöglichkeit für komplexe Zahlen. Anstatt Real- und Imaginärteil anzugeben, stellt man eine komplexe Zahl z durch ihre Länge r im komplexen Koordinatensystem und den Winkel (f) dar, den der Vektor mit der reellen Achse einschließt. Diese Form der Darstellung nennt man die Polarform einer komplexen Zahl (Satz von Pythagoras).

Die Länge des Vektors ist

r = = (Funktion IMABS)

Eine komplexe Zahl z lässt sich folgendermaßen darstellen:

Es gilt:

Re(z) = a = rcos (f) (Funktion IMREAL)

Im(z) = ib = rsin (f) (Funktion IMAGINARY)

Daraus folgt:

z = Re(z) + Im(z) = r(cos (f) + sin (f)) (Funktion COMPLEX)

8.3 Rechenregeln

8.3.1 Addition und Subtraktion

Man kann mit komplexen Zahlen fast genauso rechnen, wie mit reellen Zahlen. Dazu lässt man i einfach als Variable stehen.

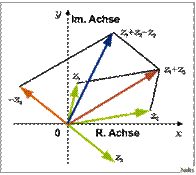
Figure 3: Addition und Subtraktion komplexer Zahlen

Die Addition bzw. Subtraktion zweier Zahlen z = a + bi und w = c + di funktioniert folgendermaßen:

z ± w = (a + bi) ± (c + di) = (a + c) ± (bi + di) = (a + c) ± (b + d)i

Man kann also zwei komplexe Zahlen addieren, indem man ihre Realteile und ihre Imaginärteile einzeln addiert bzw. subtrahiert.

Beispiel:

(3 + 7i) + (5 + 2i) = 8 + 9i

(3 + 7i) – (5 + 2i) = -2 + 5i

8.3.2 Multiplikation und Division

Auch für die Multiplikation gelten die gleichen Regeln wie bei reellen Zahlen. Bei der Multiplikation und Division ist zu beachten, dass i² = -1 ist.

zw = (a + bi)(c + di) = ac + adi + bic + bidi = ac + (ad + bc)i + bdi²

Weil i so definiert, dass i² = -1 ist, gilt:

zw = ac + (ad + bc)i + bdi² = ac - bd + (ad + bc)i

Beispiel:

(3 + 7i)(5 - 2i) = 15 –(14 i²) + [3(-2) + 35]i = 15 + 14 + (-6 + 35)i = 29 + 29i

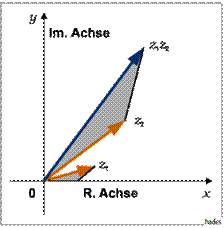
Figure 4: Multiplikation von komplexen Zahlen

Man kann eine komplexe Zahl auch mit sich selbst multiplizieren, also quadrieren:

z² = (a + bi)² = aa - bb + (ab + ba)i = a² - b² + 2abi

Beispiel:

(5 – 2i)² = 5² - (-2)² + 10(-2)i = 25 - 4 + (-20)i = 21 - 20i

Bei der Division zweier komplexer Zahlen muss der Nenner geeignet erweitert werden.

8.4 Funktionen im Excel 2000

8.4.1 Imreal (Imrealteil)

Diese Funktion liefert den Realteil einer komplexen Zahl, die als Zahlenfolge x + yi oder x + yj eingegeben wird.

Syntax:

=IMREAL(inumber)

=IMREALTEIL(Komplexe Zahl)

Beispiel:

=IMREAL("7-8i") ergibt 7

8.4.2 Imaginary (Imaginärteil)

Diese Funktion liefert den Imaginärteil einer komplexen Zahl.

Syntax:

=IMAGINARY(inumber)

=IMAGINÄRTEIL(Komplexe Zahl)

Beispiel:

=IMAGINARY("7-8i") ergibt 8

8.4.3 Complex (Komplexe)

Mit Hilfe dieser Funktion wird der Real- und der Imaginärteil in eine komplexe Zahl umgewandelt.

Syntax:

=COMPLEX(Real_num; I_num; suffix)

=KOMPLEXE(Realteil; Imaginärteil; Suffix)

Suffix: ist der Buchstabe, der für die imaginäre Einheit der komplexen Zahlen (i bzw. j) verwendet werden soll. Fehlt das Argument Suffix, wird es als "i" angenommen.

Beispiele:

Figure 5: Zusammensetzung einer komplexen Zahl

=COMPLEX(5; 8; "j") ergibt 5 + 8j

8.4.4 Imconjugate (Imkonjugierte)

Diese Funktion liefert die konjugiert komplexe Zahl zu einer komplexen Zahl.

Syntax:

=IMCONJUGATE(inumber)

=IMKONJUNGIERTE(Komplexe Zahl)

Beispiel:

=IMCONJUGATE("6 + 3i") ergibt 6 – 3i

8.4.5 Imabs (Imabs)

Liefert den Absolutbetrag (Modulus) einer komplexen Zahl.

Syntax:

=IMABS(inumber)

=IMABS(Komplexe Zahl)

Beispiel:

z = 5 + 12i

r = 13

=IMABS("5 + 12i") ergibt 13

8.4.6 Imsum (Imsumme)

Liefert die Summe komplexer Zahlen.

Syntax:

=IMSUM(inumber 1; inumber 2,...)

=IMSUMME(Komplexe Zahl 1; Komplexe Zahl 2,…)

Beispiel:

(a + bi) + (c + di) = (a + c) + (b + d)i

=IMSUM("6 + 3i"; "5 + i") ergibt 11 + 4i

8.4.7 Imsub (Imsub)

Liefert die Differenz zweier komplexer Zahlen.

Syntax:

=IMSUB(inumber 1; inumber 2,...)

=IMSUB(Komplexe Zahl 1; Komplexe Zahl 2,…)

Beispiel:

(a + bi) – (c + di) = (a – c) + (b – d)i

=IMSUB("6 + 3i"; "5 + i") ergibt 1 + 2i

8.4.8 Improduct (Improdukt)

Liefert das Produkt komplexer Zahlen.

Syntax:

=IMPRODUCT(inumber 1; inumber 2,...)

=IMPRODUKT(Komplexe Zahl 1; Komplexe Zahl 2,…)

Beispiel:

(a + bi)(c + di) = (ac – bd) + (ad + bc)i

=IMPRODUCT("3 + 4i")("5 – 3i") = 15 – 9i + 20i – 12 i²

= 15 + 11i +12

= 27 + 11i

=IMPRODUCT("5 + 3i")("3 – 2i") = 15 + 9i – 10i – 6i²

= 15 – i +6

= 21 – i

8.4.9 Imdiv (Imdiv)

Liefert den Quotienten zweier komplexer Zahlen.

Syntax:

=IMDIV(inumber 1; inumber2)

=IMDIV(Komplexe Zahl 1; Komplexe Zahl 2)

Komplexe Zahl 1 = der komplexe Zähler oder der Dividend.

Komplexe Zahl 2 = der komplexe Nenner oder Divisor.

Beispiel:

IMDIV (z₁, z₂) =

8.4.10 Imsqrt (Imwurzel)

Liefert die Quadratwurzel einer komplexen Zahl.

Syntax:

=IMSQRT(inumber)

=IMWURZEL(Komplexe Zahl)

Beispiel:

=IMSQRT("6 + 3i") ergibt 2,520734 + 0,595065i

8.4.11 Imargument (Imargument)

Gibt das Argument, ausgedrückt im Winkel Theta, als Bogenmaß an.

Syntax:

=IMARGUMENT(inumber)

=IMARGUMENT(Komplexe Zahl)

Beispiel:

IMARGUMENT (z) =Theta

=IMARGUMENT("10 + 4i") ergibt 0,380506 (Rad).

Grad =

=21,8 º

8.4.12 Imsin (Imsin) bzw. Imcos (Imcos)

Imsin liefert den Sinus, die Funktion Imcos den Kosinus einer komplexen Zahl.

Syntax:

=IMSIN(inumber) =IMSIN(Komplexe Zahl)

=IMCOS(inumber) =IMCOS(Komplexe Zahl)

Beispiel:

=IMSIN("3 + 2i") ergibt 0,530921 – 3,590565i

=IMCOS("5 + 2i") ergibt 1,067193 + 3,477884i

8.4.13 Impower (Imapotenz)

Potenziert eine komplexe Zahl.

Syntax:

=IMPOWER(inumber; number)

=IMAPOTENZ(Komplexe Zahl; Potenz)

Die Potenz kann eine ganze Zahl sein, eine rationale Zahl (Bruchzahl) oder negativ sein.

8.4.14 Imexp (Imexp)

Diese Funktion liefert die algebraische Form einer in exponentieller Form vorliegenden komplexen Zahl.

Syntax:

=IMEXP(inumber)

=IMEXP(Komplexe Zahl)

Beispiel:

Für eine in exponentieller Schreibweise vorliegende komplexe Zahl gilt wegen der Eulerschen Formel:

IMEXP (z) =

=IMEXP("1 + 5i") ergibt 0,771074 – 2,606626i

8.4.15 Imln, Imlog2, Imlog10

Imln liefert den natürlichen Logarithmus, Imlog2 den Logarithmus zur Basis 2, Imlog10 den Logarithmus zur Basis 10, einer komplexen Zahl.

Syntax:

=IMLN(inumber) =IMLN(Komplexe Zahl)

=IMLOG2(inumber) =IMLOG2(Komplexe Zahl)

=IMLOG10(inumber) =IMLOG10(Komplexe Zahl)

8.5 Quellenverzeichnis

8.5.1 Inhalte

Excel XP Hilfe

„Excel, Grundlagen Tabellenkalkulation“, Herdt-Verlag, 3.Auflage Jänner 2000

„Excel, Fortgeschrittene Anwendungen“, Herdt-Verlag, 3.Auflage Februar 2000

http://iwi.uibk.ac.at/ftp/Jarz/

http://home.pages.at/cramer/excel/start.htm

8.5.2 Beispiele

http://www.gm.fh-koeln.de/~wwwfb19/boehm/public/download.htm

http://www.wipnet.at/db/db287.asp

[1] Annuität: Ist ein Tilgungsanteil, der sich aus den Zinsen und dem konstanten Betrag zusammensetzt, der in einer Periode zu entrichten ist.